Ca mecanism de transmisie, angrenajul planetar este utilizat pe scară largă în diverse practici inginerești, cum ar fi reductoarele cu angrenaje, macaralele, reductoarele planetare etc. În cazul reductoarelor planetare, acestea pot înlocui mecanismul de transmisie al trenului de angrenaje cu axă fixă ​​în multe cazuri. Deoarece procesul de transmisie a angrenajului este prin contact liniar, angrenarea pe termen lung va cauza defectarea angrenajului, așa că este necesară simularea rezistenței acestuia. Li Hongli și colab. au utilizat metoda automată de angrenare pentru a angrena angrenajul planetar și au obținut că cuplul și tensiunea maximă sunt liniare. Wang Yanjun și colab. au angrenat, de asemenea, angrenajul planetar prin metoda de generare automată și au simulat simularea statică și modală a angrenajului planetar. În această lucrare, elementele tetraedrice și hexaedrice sunt utilizate în principal pentru a diviza angrenajul, iar rezultatele finale sunt analizate pentru a vedea dacă sunt îndeplinite condițiile de rezistență.

1. Stabilirea modelului și analiza rezultatelor

Modelarea tridimensională a angrenajului planetar

Angrenaj planetareste compus în principal din coroană dințată, roată dințată solară și roată dințată planetară. Principalii parametri selectați în această lucrare sunt: ​​numărul de dinți ai coroanei dințate interioare este de 66, numărul de dinți ai roții dințate solare este de 36, numărul de dinți ai roții dințate planetare este de 15, diametrul exterior al coroanei dințate interioare este de 150 mm, modulul este de 2 mm, unghiul de presiune este de 20°, lățimea dintelui este de 20 mm, coeficientul de înălțime adițională este de 1, coeficientul de joc este de 0,25 și există trei roți dințate planetare.

Analiza statică prin simulare a angrenajului planetar

Definiți proprietățile materialului: importați sistemul de angrenaje planetare tridimensional desenat în software-ul UG în ANSYS și setați parametrii materialului, așa cum se arată în Tabelul 1 de mai jos:

Discretizare: Discreția cu elemente finite este împărțită prin tetraedru și hexaedru, iar dimensiunea de bază a elementului este de 5 mm. Deoareceangrenaj planetar, roata dințată solară și inelul dințat interior sunt în contact și angrenează, plasa părților de contact și a plasei este densificată, iar dimensiunea este de 2 mm. Mai întâi, se utilizează grile tetraedrice, așa cum se arată în Figura 1. Sunt generate în total 105906 elemente și 177893 noduri. Apoi se adoptă grila hexaedrică, așa cum se arată în Figura 2, și sunt generate în total 26957 celule și 140560 noduri.

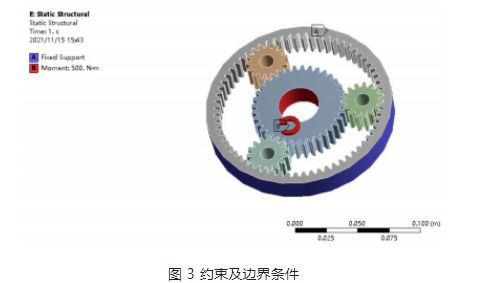
Aplicarea sarcinii și condițiile limită: în funcție de caracteristicile de funcționare ale angrenajului planetar din reductor, angrenajul solar este angrenajul acționat, angrenajul planetar este angrenajul antrenat, iar ieșirea finală se face prin intermediul suportului planetar. Fixați inelul dințat interior în ANSYS și aplicați un cuplu de 500 N · m la angrenajul solar, așa cum se arată în Figura 3.

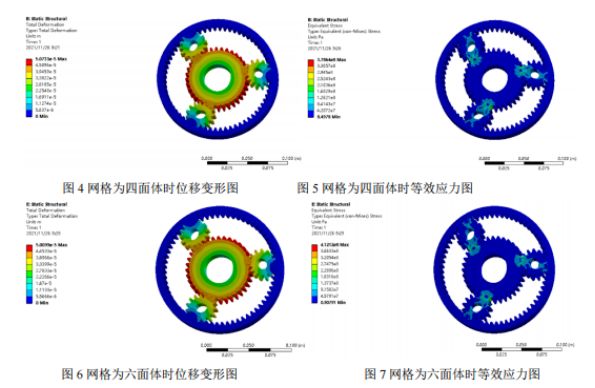
Postprocesare și analiza rezultatelor: Mai jos sunt prezentate nefograma de deplasare și nefograma de tensiune echivalentă obținute din două diviziuni ale grilei, iar este efectuată o analiză comparativă. Din nefograma de deplasare a celor două tipuri de grile, se constată că deplasarea maximă are loc în poziția în care roata solară nu se angrenează cu roata planetară, iar tensiunea maximă are loc la rădăcina angrenajului. Tensiunea maximă a grilei tetraedrice este de 378 MPa, iar tensiunea maximă a grilei hexaedrice este de 412 MPa. Deoarece limita de curgere a materialului este de 785 MPa, iar factorul de siguranță este de 1,5, tensiunea admisibilă este de 523 MPa. Tensiunea maximă pentru ambele rezultate este mai mică decât tensiunea admisibilă și ambele îndeplinesc condițiile de rezistență.

2. Concluzie

Prin simularea cu elemente finite a angrenajului planetar se obțin nefograma deplasării-deformare și nefograma tensiunii echivalente a sistemului de angrenaje, din care se obțin datele maxime și minime și distribuția acestora în...angrenaj planetarse poate găsi modelul. Locația tensiunii echivalente maxime este și locația în care dinții angrenajului sunt cel mai probabil să se rupă, așa că trebuie acordată o atenție specială acesteia în timpul proiectării sau fabricației. Prin analiza întregului sistem de angrenaje planetare, se depășește eroarea cauzată de analiza unui singur dinte de angrenaj.